INDICADORES DE LOGRO
1.1 Establece
relaciones entre conjuntos y realiza diferentes operaciones.
1.2 Describe y
desarrolla algoritmos, para hacer estimaciones y cálculos de potenciación,
radicación y logaritmación.
1.3 Usa los conceptos
de plano cartesiano, transformaciones rígidas, semejanza y congruencia para
modelar situaciones geométricas.
1.4 Realiza
conversiones de unidades de medida y usa las unidades de longitud para hallar
el perímetro de figuras geométricas compuestas.
1.5 Resuelve
situaciones problema usando las operaciones entre números naturales y los
conceptos de la teoría de números.
1.6 Asume con
disciplina, responsable y puntualmente el desarrollo de guías, talleres,
tareas, evaluaciones, corrección de evaluaciones y material didáctico
suministrado por el docente; para fortalecer el conocimiento matemático.
1.7 Acepta con interés
y respeto el pensamiento de los compañeros mediante la valoración crítica y
constructiva del conocimiento matemático para fortalecer el trabajo del grupo y
la convivencia.
|
REFERENTES CONCEPTUALES |
|
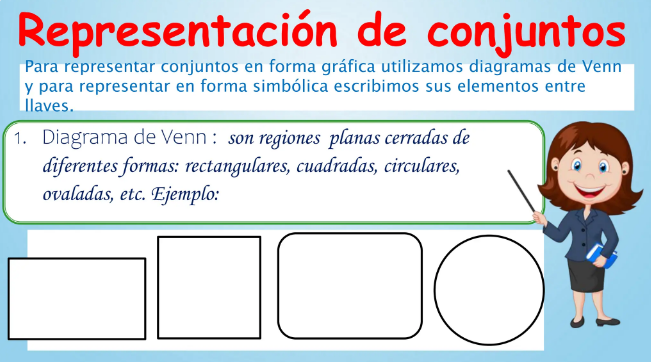
PENSAMIENTO NUMÉRICO CONJUNTOS ·
Representación, determinación y clases de conjuntos. · Operaciones
entre conjuntos OPERACIONES CON NÚMEROS ·
Adición y Sustracción. ·
Multiplicación y División. TEORÍA DE NÚMEROS ·
Descomposición factorial. ·
Máximo y Mínimo común múltiplo. ·
Potenciación. ·
Radicación. · Logaritmación. PENSAMIENTO GEOMÉTRICO ESPACIAL GENERALIDADES DE GEOMETRÍA ·
Movimientos en el plano cartesiano. ·
Plano cartesiano. ·
Traslaciones, Rotaciones y Reflexiones. ·
Congruencia y Semejanza. PENSAMIENTO MÉTRICO MEDIDAS
DE LONGITUD ·
El metro. ·
Múltiplos y submúltiplos del metro. ·
Conversiones entre unidades de longitud. · Perímetro de figuras geométricas. |
NOTACIÓN DE CONJUNTO POR EXTENSION Y POR COMPRENSIÓN
El siguiente video nos explica de forma muy detallada la diferencia entre estas dos notaciones, aclara tus inquietudes 👍 AQUÍ
OPERACIONES ENTRE CONJUNTOS
Este video nos muestra operaciones combinadas de UNIÓN e INTERSECCIÓN entre conjuntos
Míralo 👉 AQUÍ
Este video nos muestra operaciones combinadas con la DIFERENCIA y COMPLEMENTO entre conjuntos
Míralo 👉 AQUÍ
💢💢💢
¿Qué es la diferencia simétrica entre dos conjuntos?
Descúbrelo en este VIDEO
Solución de situaciones matemáticas con conjuntos
En el siguiente video vemos la aplicación del tema de conjuntos para
solucionar situaciones matemáticas:
Comparto video tutoriales que les ayudará a recordar procesos de división entre dos y tres cifras:
Los criterios de divisibilidad son pautas que nos permiten saber rápidamente si un número es divisible entre otro. Es decir, nos permiten saber si cuando los dividamos el resto de la división será cero o no.
Los criterios de divisibilidad son muy útiles
- Nos ayudan a encontrar con facilidad los divisores de un número.
- Nos sirven especialmente cuando tenemos que descomponer números en factores primos o saber si un número es primo o compuesto.
- Nos dan pistas cuando tenemos que simplificar fracciones, entre muchas otras cosas…
Criterios de divisibilidad del 2
Para saber si un número es divisible entre dos hay que comprobar que termine en cero o número par. Si es par, entonces será divisible por 2. Los número pares son los que terminan en 0, 2, 4, 6 y 8.
Ejemplo:
- ¿316 es divisible entre 2? Si miramos el último número, vemos que el 6 es un número par, por lo tanto 316 es divisible entre 2.
Criterios de divisibilidad del 3
a. ¿45 es divisible por 3? Una forma de saberlo es dividir 45 entre 3:
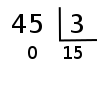
Como el resto de la división es cero, podemos decir que 45 es divisible por 3.
Como ya sabemos que 45 es divisible por 3 vamos a comprobar que la suma de sus cifras es un múltiplo de 3.
- Sumamos sus cifras: 45 –> 4 + 5 = 9
- 9 es divisible por 3 por lo tanto 45 también es divisible por 3.
b. ¿5898521456985 es divisible por 3?
- Sumamos todas sus cifras: 5 + 8 + 9 + 8 + 5 + 2 + 1 + 4 + 5 + 6 + 9 + 8 + 5 = 75
- 7 + 5 = 12
- 12 es divisible por 3, por lo tanto 5898521456985 sí es divisible por 3.
Criterios de divisibilidad del 4
Ejemplo:
- ¿528 es divisible entre 4? Si miramos los dos últimos números, vemos que el 28 es un número múltiplo de 4 (4X7 es igual a 28), por lo tanto 528 es divisible entre 4.
Criterio de divisibilidad del 5
Para saber si un número es divisible entre 5, dicho número tiene que terminar en 0 o 5.
Ejemplo:
- ¿5815 es divisible entre 5? Miramos el último número y es un 5, por lo tanto, 5815 es divisible entre 5.
Criterios de divisibilidad del 6
Para saber si un número es divisible por 6 tiene que cumplir dos condiciones:
- Tiene que ser divisible por 2, es decir, tiene que ser un número par.
- Tiene que ser divisible por 3, es decir, la suma de sus dígitos tiene que ser 3 o múltiplo de 3.
¿Es 3654 divisible por 6?
Comprobamos los dos criterios:
- ¿Es divisible por 2? Sí, porque termina en número par.
- ¿Es divisible por 3? Sí, porque 3+6+5+4=18, y 18 es múltiplo de 3.
Como se cumplen las 2 condiciones, 3654 sí es divisible por 6.
Criterios de divisibilidad del 7
Para saber si un número es divisible por 7 hay que restar el número sin la cifra de las unidades y el doble de la cifra de las unidades. Si el resultado es cero o múltiplo de 7 entonces el número es divisible por 7. Si el resultado es diferente, el número no es divisible por 7.
Vemos con un ejemplo:
¿1946 es divisible por 7?
Separamos la cifra de las unidades 194 / 6
Ahora restamos el número 194 menos el doble de la cifra de las unidades 2×6 = 12
194 – 12 = 182
Como 182 todavía es un número muy grande, repetimos los pasos:
Separamos la cifra de las unidades 18 / 2
Restamos el número 18 menos el doble de la cifra de las unidades 2×2=4
18 – 4 = 14
14 es un múltiplo de 7. Por lo tanto 1946 sí es divisible por 7.
Criterio de divisibilidad del 10
Para saber si un número es divisible entre 10, éste tiene que terminar en 0. Un número es divisible entre 10, si es divisible entre 2 y 5 al mismo tiempo.
Ejemplo:
- ¿370 es divisible entre 10? El último número es un 0, por lo tanto 370 sí es divisible entre 10. 370 tambien es divisible entre 2 y 5.
¿Qué es una potencia?
Las potencias sirven para escribir una multiplicación formada por varios números iguales de una manera más simplificada.
Por ejemplo, 5 x 5 x 5 x 5. Estamos multiplicando 4 veces el número 5.
Para ponerlo en forma de potencia escribimos primero el 5 y arriba a la derecha escribimos el 4 en pequeño.
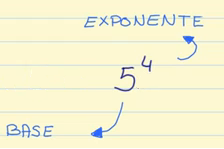
Términos de una potencia
El 5 es la base, que es el número que se multiplica y el 4 es el exponente, que es el número de veces que se multiplica la base.
Esto se lee: 5 elevado a 4.
¿Qué son los números primos?
Definimos los números primos como aquellos que solo se pueden dividir por sí mismos o por la unidad, es decir, son números naturales mayores que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1.
¿Qué son los números compuestos?
Al contrario que los números primos, los compuestos son aquellos números naturales que, además de poder dividirse por ellos mismos y la unidad, también son divisibles por otros números.
Como resumen, diremos que los números primos solo tienen dos divisores, mientras que los números compuestos pueden tener tres o más.
👍👍👍
Descomposición en factores primos
Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.
Para descomponer un número en producto de factores primos se siguen estos pasos:
1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
Ejemplo 1: Realiza la descomposición en producto de factores primos del número 24:
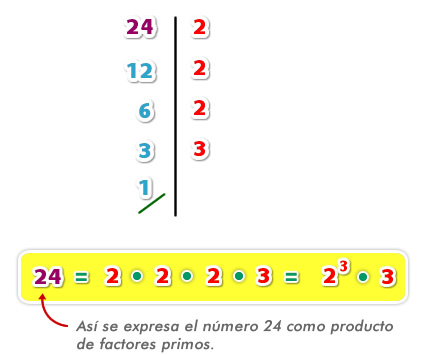
¿Qué es el mínimo común múltiplo (mcm)?
El mínimo común múltiplo (mcm) es el número positivo más pequeño que es múltiplo de dos o más números.
Para entender mejor esta definición vamos a ver todos los términos.
Múltiplo
Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.
Vamos a ver un ejemplo de los múltiplos de 2 y de 3. Para calcular sus múltiplos hay que ir multiplicando el 2 y el 3 por 1, por 2, por 3, etc.
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
y así sucesivamente hasta infinitos números.
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
y así sucesivamente hasta infinitos números.

Múltiplo Común
Un múltiplo común es un número que es múltiplo a la vez de dos o más números, es decir, es un múltiplo común a esos números.
Siguiendo con el ejemplo anterior, vamos a ver los múltiplos comunes de 2 y de 3.

Habrá que ver qué múltiplos tienen en común el dos y el tres, que en la imagen figuran en verde, es decir, el 6, el 12 y el 18. Hay que tener en cuenta que los múltiplos son infinitos y que nosotros solo hemos mostrado los primeros de cada número.
Mínimo común múltiplo
El mínimo común múltiplo es el número más pequeño de los múltiplos comunes.
Siguiendo con el ejemplo anterior, si los múltiplos comunes de 2 y de 3 eran 6, 12 y 18, el mínimo común múltiplo o mcm es 6, ya que es el menor de los múltiplos comunes.
Cómo calcular el mínimo común múltiplo
Se pueden utilizar dos métodos.
- El primer método para calcular el mcm es el que hemos utilizado antes, es decir, escribimos los primeros múltiplos de cada número, señalamos los múltiplos que sean comunes y elegimos el múltiplo común más pequeño.
- Ahora vamos a explicar el segundo método para calcular el mcm. Lo primero que hay que hacer es descomponer en factores primos cada número. Después tendremos que elegir los factores comunes y no comunes elevados al mayor exponente y por último, tendremos que multiplicar los factores elegidos.
Vamos a ver un ejemplo de esto, calculando el mcm de 12 y de 8.
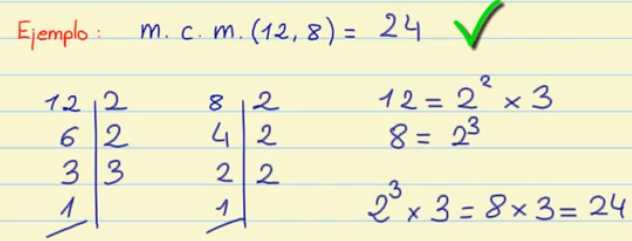
Vamos a descomponer 12 y 8 en factores primos:
12 = 22 x 3
8 = 23
Ahora elegimos los factores comunes y no comunes elevados al mayor exponente, por lo tanto elegimos 23 y el 3.
Y por último los multiplicamos, por lo tanto 23 x 3 = 8 x 3 = 24
Así que el mcm ( 12 , 8 ) = 24
Video que nos fortalece el proceso para calcular el mínimo común múltiplo
💢💢💢
Semana del 3 de marzo de 2025
¿Qué es la radicación?
La radicación es la forma como se expresa que un número debe multiplicarse por sí mismo, la cantidad de veces que otro número se lo indique, para obtener un valor exacto de esta operación.
Por eso en la radicación siempre hay tres números que juegan un papel muy importante y dependen los unos de los otros. Estos son sus nombres:
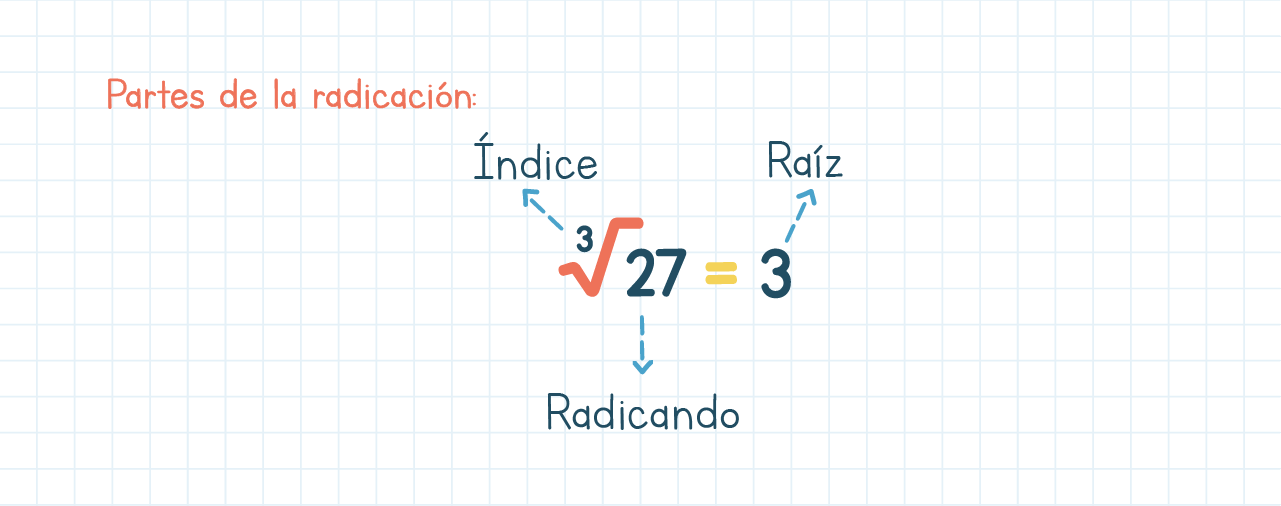
- La raíz es el número que debe multiplicarse por sí mismo, las veces que el índice se lo indique.
- El radicando es el resultado de la operación entre índice y raíz.
¿Cómo encontrar el resultado de una radicación?
Imagina que no conoces el resultado del ejemplo anterior, de hecho, siempre que te enfrentes a una radicación te darán el índice y el radicando. Así:
%204.25.58%20p.m..png)
Entonces, la pregunta qué debes hacerte es: ¿cuál es el número que multiplicado veces te da como resultado ?
Prueba con el :
Claramente este número no te sirve.
Intenta con el ...
¡Exacto! El resultado indicado es el . Eso significa que la raíz cúbica de 27 es 3.

Básicamente, se trata de buscar, probar y jugar un poco con los números hasta encontrar esa raíz exacta que estás buscando.
¿Cómo se lee la radicación?
- Cuando el índice es un , se debe leer "raíz cuadrada de…"
- Cuando el índice es un , se dice "raíz cúbica de…"
- Cuando el índice es diferente a los números y , se lee "raíz cuarta de...", "raíz quinta de...", y así sucesivamente.
Radicación I: cálculo de raíces básicas
💢💢💢
Semana del 10 de marzo de 2025
¿Qué es la logaritmación?
La logaritmación es una operación inversa a la potenciación.
La logaritmación permite calcular el exponente cuando se conocen la base y la potencia.
Se escribe: Log2 32=5
Se lee: Logaritmo en base 2 de 32 es igual a 5
Se verifica: 2 x 2 x 2 x 2 x 2 = 32
💢💢💢
Día Internacional de las matemáticas
14 de marzo
Una mayor conciencia mundial y un fortalecimiento de la enseñanza de las ciencias matemáticas son esenciales para hacer frente a desafíos que se plantean en ámbitos como la inteligencia artificial, el cambio climático, la energía y el desarrollo sostenible, y para mejorar la calidad de vida en el mundo desarrollado y en el mundo en desarrollo. Por esta razón, la 40ª Conferencia General de la UNESCO proclamó el 14 de marzo de cada año como el Día Internacional de las Matemáticas en noviembre de 2019 (40C/Resolución 30).
En muchos países, el 14 de marzo (3/14) ya se celebra como el Día del Pi porque π, una de las constantes matemáticas más conocidas del mundo, puede redondearse a 3,14.
Fuente: UNESCO, 2023
Video: ¿Las matemáticas las descubrimos o las inventamos?
Un milerio debate sin resolver
¿Quieres saber para que sirve el número pi ?
💢💢💢
Mira que interesante: