Bienvenidos al segundo
periodo académico 2025
MATEMÁTICAS 4to Grado
Durante el segundo periodo académico, es necesario apreciado estudiante reforzar las operaciones básicas. Le invito a generar estratégicas académicas que le ayuden con el aprendizaje de las tablas de multiplicar (en desorden).
A continuación, le comparto ejercicios de refuerzo que le ayudarán a complementar su aprendizaje.
Ejercicios (Da click sobre cada tema)
Cordial saludo.
Les recomiendo su lectura completa, apropiación de la información y atención a las fechas que definen las actividades académicas del segundo periodo y próximos.
Por favor acompañar a sus hijos en la preparación para las próximas fechas de evaluaciones acumulativas, a desarrollarse
SEMANA DEL 26 DE MAYO:
Cordialmente,
Constanza Ríos Contreras
Docente de aula matemáticas
Los criterios de divisibilidad son pautas que nos permiten saber rápidamente si un número es divisible entre otro. Es decir, nos permiten saber si cuando los dividamos el resto de la división será cero o no.
Los criterios de divisibilidad son muy útiles
- Nos ayudan a encontrar con facilidad los divisores de un número.
- Nos sirven especialmente cuando tenemos que descomponer números en factores primos o saber si un número es primo o compuesto.
- Nos dan pistas cuando tenemos que simplificar fracciones, entre muchas otras cosas…
Criterios de divisibilidad del 2
Para saber si un número es divisible entre dos hay que comprobar que termine en cero o número par. Si es par, entonces será divisible por 2. Los número pares son los que terminan en 0, 2, 4, 6 y 8.
Ejemplo:
- ¿316 es divisible entre 2? Si miramos el último número, vemos que el 6 es un número par, por lo tanto 316 es divisible entre 2.
Criterios de divisibilidad del 3
a. ¿45 es divisible por 3? Una forma de saberlo es dividir 45 entre 3:
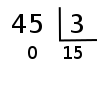
Como el resto de la división es cero, podemos decir que 45 es divisible por 3.
Como ya sabemos que 45 es divisible por 3 vamos a comprobar que la suma de sus cifras es un múltiplo de 3.
- Sumamos sus cifras: 45 –> 4 + 5 = 9
- 9 es divisible por 3 por lo tanto 45 también es divisible por 3.
b. ¿5898521456985 es divisible por 3?
- Sumamos todas sus cifras: 5 + 8 + 9 + 8 + 5 + 2 + 1 + 4 + 5 + 6 + 9 + 8 + 5 = 75
- 7 + 5 = 12
- 12 es divisible por 3, por lo tanto 5898521456985 sí es divisible por 3.
Criterios de divisibilidad del 4
Ejemplo:
- ¿528 es divisible entre 4? Si miramos los dos últimos números, vemos que el 28 es un número múltiplo de 4 (4X7 es igual a 28), por lo tanto 528 es divisible entre 4.
Criterio de divisibilidad del 5
Para saber si un número es divisible entre 5, dicho número tiene que terminar en 0 o 5.
Ejemplo:
- ¿5815 es divisible entre 5? Miramos el último número y es un 5, por lo tanto, 5815 es divisible entre 5.
Criterios de divisibilidad del 6
Para saber si un número es divisible por 6 tiene que cumplir dos condiciones:
- Tiene que ser divisible por 2, es decir, tiene que ser un número par.
- Tiene que ser divisible por 3, es decir, la suma de sus dígitos tiene que ser 3 o múltiplo de 3.
¿Es 3654 divisible por 6?
Comprobamos los dos criterios:
- ¿Es divisible por 2? Sí, porque termina en número par.
- ¿Es divisible por 3? Sí, porque 3+6+5+4=18, y 18 es múltiplo de 3.
Como se cumplen las 2 condiciones, 3654 sí es divisible por 6.
Criterios de divisibilidad del 7
Para saber si un número es divisible por 7 hay que restar el número sin la cifra de las unidades y el doble de la cifra de las unidades. Si el resultado es cero o múltiplo de 7 entonces el número es divisible por 7. Si el resultado es diferente, el número no es divisible por 7.
Vemos con un ejemplo:
¿1946 es divisible por 7?
Separamos la cifra de las unidades 194 / 6
Ahora restamos el número 194 menos el doble de la cifra de las unidades 2×6 = 12
194 – 12 = 182
Como 182 todavía es un número muy grande, repetimos los pasos:
Separamos la cifra de las unidades 18 / 2
Restamos el número 18 menos el doble de la cifra de las unidades 2×2=4
18 – 4 = 14
14 es un múltiplo de 7. Por lo tanto 1946 sí es divisible por 7.
Criterio de divisibilidad del 10
Para saber si un número es divisible entre 10, éste tiene que terminar en 0. Un número es divisible entre 10, si es divisible entre 2 y 5 al mismo tiempo.
Ejemplo:
- ¿370 es divisible entre 10? El último número es un 0, por lo tanto 370 sí es divisible entre 10. 370 tambien es divisible entre 2 y 5.
¿Qué es una potencia?
Las potencias sirven para escribir una multiplicación formada por varios números iguales de una manera más simplificada.
Por ejemplo, 5 x 5 x 5 x 5. Estamos multiplicando 4 veces el número 5.
Para ponerlo en forma de potencia escribimos primero el 5 y arriba a la derecha escribimos el 4 en pequeño.
Términos de una potencia
El 5 es la base, que es el número que se multiplica y el 4 es el exponente, que es el número de veces que se multiplica la base.
Esto se lee: 5 elevado a 4.
¿Qué son los números primos?
Definimos los números primos como aquellos que solo se pueden dividir por sí mismos o por la unidad, es decir, son números naturales mayores que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1.
¿Qué son los números compuestos?
Al contrario que los números primos, los compuestos son aquellos números naturales que, además de poder dividirse por ellos mismos y la unidad, también son divisibles por otros números.
Como resumen, diremos que los números primos solo tienen dos divisores, mientras que los números compuestos pueden tener tres o más.
👍👍👍
Descomposición en factores primos
Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.
Para descomponer un número en producto de factores primos se siguen estos pasos:
1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
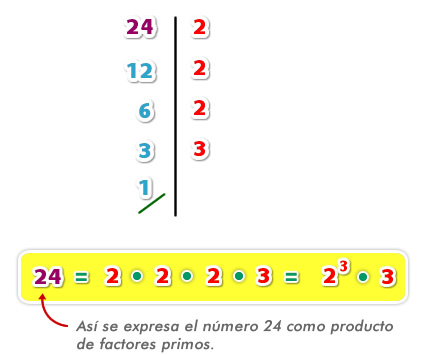
Ejemplo 1: Realiza la descomposición en producto de factores primos del número 24:
Triángulos
Son los polígonos de tres lados. Se pueden clasificar:
- Según sus lados: equilátero, isósceles y escaleno.
- Según sus ángulos: equiángulo, acutángulo y obtusángulo.